how to find the length of a triangle
FINDING THE MISSING LENGTH OF A Right TRIANGLE
If the lengths of two sides of a correct triangle are given, we tin can employ Pythagorean Theorem to find the length of the missing side.
Pythagorean Theorem :
Square of the hypotenuse of a right triangle is equal to sum of the squares of other two sides.
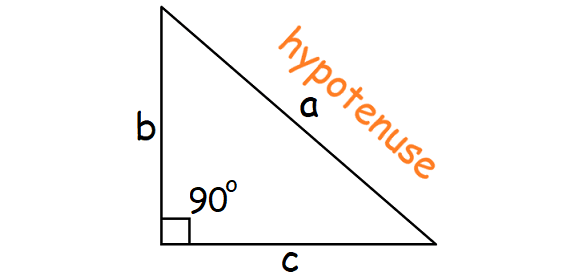
a2 = bii + c2
If you know the values of any two variables, y'all can solve for the 3rd variable using the above equation.
Note :
Hypotenuse is the longest side of a correct triangle and information technology is ever opposite to the correct angle.
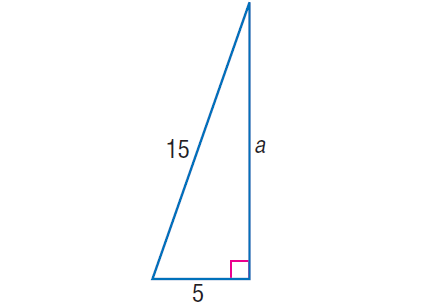
Example 1 :
In the right triangle shown beneath, find the value of 'a'.
Solution :
In the correct triangle above, past Pythagorean Theorem,
xv2= 5ii + a2
225 = 25 + aii
Decrease 25 from both sides.
200 = a 2
Take square root on both sides.
√200 = √a2
√(2 x 10 x 10) = a
10√2 = a
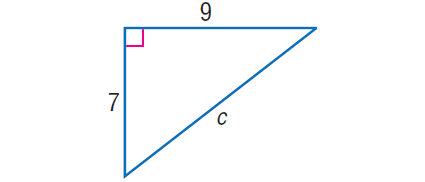
Case two :
In the correct triangle shown below, notice the value of 'c'.
Solution :
In the right triangle above, by Pythagorean Theorem,
cii= seven2 + 92
c2= 49 + 81
c2= 130
Accept square root on both sides.
√ c2 = √130
c =√130
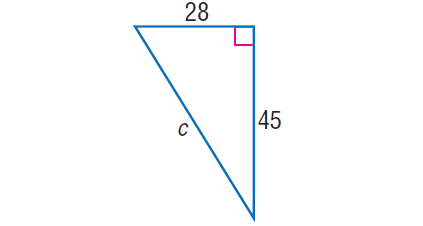
Example 3 :
In the correct triangle shown below, find the value of 'c'.
Solution :
In the right triangle above, by Pythagorean Theorem,
cii= 282 + 452
c2= 784 + 2025
cii= 2809
Take square root on both sides.
√ c = √2809
c = 53
Example four :
In the right triangle shown below, find the value of 'b'.
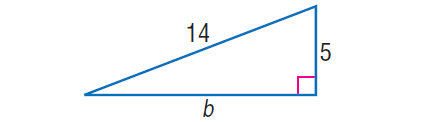
Solution :
In the right triangle in a higher place, by Pythagorean Theorem,
14 two = five2 + b2
196 = 25 + b 2
Decrease 25 from both sides.
171 = btwo
√171 =√b2
√171 = b
Case 5 :
In the correct triangle shown beneath, observe the value of 'a'.
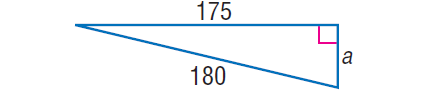
Solution :
In the correct triangle above, by Pythagorean Theorem,
180 2= aii + 1752
32400 =a ii + 30625
Subtract 30625 from both sides.
1775 = a 2
√ 1775 = √ a 2
√(5 x 5 x 71) = a
five√71 = a
Case 6 :
In the right triangle shown beneath, find the value of 'b'.
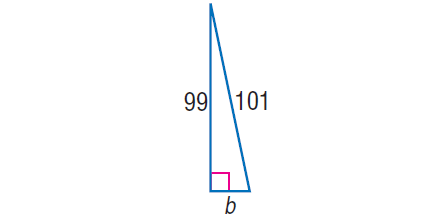
Solution :
In the correct triangle to a higher place, by Pythagorean Theorem,
101 2 = b2 + 992
10201 = b 2 + 9801
Subtract 9801 from both sides.
400 = b ii
√400 = √b2
20 = b
Example 7 :
Let a, b and c be the lengths of the sides of a right triangle. If a = 16, b = 63 and c is the length of hypotenuse, then discover the value of c.
Solution :
By Pythagorean Theorem,
c 2 = a 2 + b 2
Substitute a = sixteen and b = 63.
c2= 162 + 632
cii= 256 + 3969
cii= 4225
Take foursquare root on both sides.
√ c2 = √4225
c = 65
Example 8 :
Let a, b and c exist the lengths of the sides of a right triangle. If a = 16, c = 34 and c is the length of hypotenuse, and so discover the value of b.
Solution :
Past Pythagorean Theorem,
c 2 = a ii + b two
Substitute a = 16 and c = 34.
342= 16ii + b2
1156 = 256 + bii
Subtract 256 from both sides.
900 = b 2
Accept square root on both sides.
√ 900 = √ b 2
30 = b
Case 9 :
Let a, b and c be the lengths of the sides of a correct triangle. If b = √ 112 , c = 3 and a is the length of hypotenuse, then find the value of a.
Solution :
By Pythagorean Theorem,
a 2 = b ii + c 2
Substitute b =√112 and c = 3.
aii= ( √112) 2 + 3 two
a2= 112 + 9
a2= 121
Accept square root on both sides.
√a 2 = √121
a = 11
Case 10 :
Let a, b and c exist the lengths of the sides of a correct triangle. If a = 7y , c = 3y and a is the length of hypotenuse, then discover the value of b in terms of y.
Solution :
atwo= b2 + c2
(7y)two= b 2 + (3y) ii
49y2 = b 2 + 9y 2
Subtract 9ytwo from both sides.
40ytwo = a 2
Take foursquare root on both sides.
√(40y 2) = √a 2
2y√10 =a
Kindly mail your feedback tov4formath@gmail.com
We e'er appreciate your feedback.
Word Bug
HCF and LCM discussion problems
Give-and-take issues on simple equations
Give-and-take problems on linear equations
Give-and-take problems on quadratic equations
Algebra give-and-take issues
Give-and-take bug on trains
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on unit price
Word bug on unit charge per unit
Word problems on comparing rates
Converting customary units word problems
Converting metric units discussion problems
Give-and-take problems on simple interest
Discussion problems on chemical compound interest
Word issues on types of angles
Complementary and supplementary angles give-and-take issues
Double facts word problems
Trigonometry word problems
Percent give-and-take problems
Turn a profit and loss word bug
Markup and markdown word issues
Decimal word issues
Give-and-take problems on fractions
Word problems on mixed fractions
One footstep equation discussion bug
Linear inequalities discussion issues
Ratio and proportion word problems
Time and work discussion problems
Word problems on sets and Venn diagrams
Word problems on ages
Pythagorean theorem give-and-take bug
Percent of a number give-and-take problems
Word bug on constant speed
Word bug on boilerplate speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Profit and loss shortcuts
Percentage shortcuts
Times tabular array shortcuts
Time, speed and altitude shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the give-and-take problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Rest when 17 power 23 is divided by 16
Sum of all three digit numbers divisible past 6
Sum of all three digit numbers divisible past seven
Sum of all iii digit numbers divisible by eight
Sum of all three digit numbers formed using i, 3, four
Sum of all 3 four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, i, 2, 3
Sum of all three four digit numbers formed using one, 2, five, 6
© All rights reserved. onlinemath4all.com
Source: https://www.onlinemath4all.com/finding-the-missing-length-of-a-right-triangle.html
Posted by: tardywellink.blogspot.com

0 Response to "how to find the length of a triangle"
Post a Comment